THIS IS THE OLD VERSION OF NORM. UNLESS YOU ARE HERE FOR A REASON, YOU SHOULD USE CURRENT VERSION.

NORM's Vowel Normalization Methods

Described here are each of the methods that are implemented in NORM. We highlight some of the major pros and cons of each method, as well as the specifics of its implementation within NORM.

Bark Difference Metric

About: The Bark Difference Metric is a vowel-intrinsic method modified from the formula developed by Syrdal and Gopal (1986). Syrdal and Gopal proposed using two dimensions. Both involved computing differences between Bark-converted values (Z). To model advancement, they used either Z₃-Z₂ or Z₂-Z₁ (i.e., Bark-converted F₃ minus Bark-converted F₂ or Bark-converted F₂ minus Bark-converted F₁). To model height, they used Z₁-Z₀ (Bark-converted F₁ minus Bark-converted F₀). Z₀ was used because, all other things being equal, F₀ tends to be higher for high vowels than for low vowels, thus minimizing the distance between F₀ and F₁ for high vowels and maximizing it for low vowels. However, the problem is that all other things are seldom equal. Intonation, tone, and consonantal influences affect F₀, as does creakiness. Those processes can be circumvented, but another factor, the effects of aging on F₀, cannot, at least not speaker- and vowel-intrinsically. As a result, the Z₃-Z₁ is substituted here for Z₁-Z₀, though Z₃-Z₂ is retained.

Implementation: NORM converts the formant values to bark using the formula (Traunmüller 1997):

Zi = 26.81/(1+1960/Fi) - 0.53

Where F_i is the value for a given formant i or the mean value for a given formant i (see Multiple Methods below). It then computes the differences Z₃ - Z₁, Z₃ - Z₂, and Z₂ - Z₁. Z₃ - Z₂ is used to plot the normalized front-back dimension and Z₃ - Z₁ is used to plot the normalized height dimension.

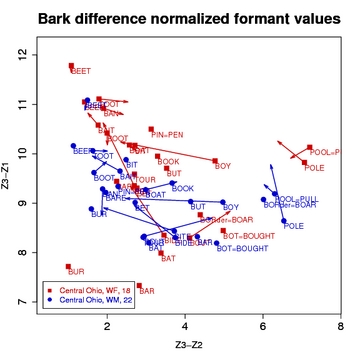Figure 1. Bark normalized vowels

Multiple Methods: NORM currently offers two versions of the Bark Difference Method. One generates normalized mean formant values, while the other generates individual normalized formant values.

Advantages/Disadvantages: In general, the Bark Difference method does a reasonable job of filtering out physiological differences while retaining sociolinguistic differences. Because the resulting plots differ in shape from those produced by vowel-extrinsic methods, it is difficult to judge whether they do a better or worse job than the vowel-extrinsic methods.

By far the biggest advantage of the Bark Difference method is that it does not require measurement of all vowels for all speakers to be included in a study. All the vowel-extrinsic methods work optimally when the entire vowel system is measured. This advantage can be crucial if a study is to include many speakers and the researcher lacks an army of research assistants to perform the acoustic measurements.

Another advantage is that the Bark Difference method (or any other vowel-intrinsic method) is that it is immune to differences in the phonological inventories of dialects or languages. That is, it cannot be skewed by comparison of systems with different vowels, e.g., a language that has front rounded vowels and one that does not. In many communities in the southern United States, where whites show fronting of BOOT and BOAT while African Americans do not, such skewing could potentially occur with vowel-extrinsic methods. Another instantiation of this advantage has to do with the "bottom corner" of the vowel envelope. Some dialects have an [a] vowel that occupies this corner (see the accompanying early NCS and Tyrone vowel sets), while other dialects do not and instead have a low front vowel [æ] and a low back vowel located across from each other (see the accompanying central Ohio and Mexican American vowel sets). Some vowel-extrinsic methods tend to set the bottom of the normalized vowel space with the lowest vowel, whatever it is, which could skew the overall vowel space depending on whether the bottom corner is occupied, but a vowel-intrinsic method cannot do so.

The most important disadvantage of the Bark Difference method is that it is heavily dependent on F₃. For some recordings, F₃ may be indistinct and hence difficult to measure--or, worse yet, faulty F₃ readings may be obtained. Furthermore, rhoticized vowels, with their low F₃, are not comparable to other vowels and have to be considered separately from the rest of the vowel inventory. If a speaker has unusual F₃ characteristics, which might result from a physiological peculiarity in the speaker's mouth dimensions or nasality in the speaker's voice, that can also skew the Bark Difference method.

Another seeming disadvantage is that the overall shape of the vowel often appears distorted. Some of the distortion is real; for example, high front unrounded vowels appear to be stretched higher than other high vowels because F₃ is higher for them than for any other vowels. Other distortions may be more apparent than real, though. Many researchers like to see a "pretty" vowel plot, which is to say that they like a plot that resembles a plot of unnormalized F₁/F₂ values. However, this preference is something of a bias because most of us are accustomed to looking at F₁/F₂ plots. If, on the other hand, we ordinarily used Hertz-difference formant plots (this isn't totally improbable--recall, for instance, that Peter Ladefoged preferred to use F₂-F₁ to represent advancement), then Bark-difference plots might not look so weird.

---

Labov ANAE Method(s)

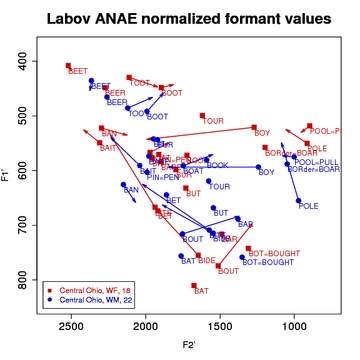Figure 2. Labov ANAE normalized vowels

About: Labov's method - the normalization approach used by the phonological Atlas of North American English - is a modification of Nearey's. While it also uses a log-mean method to normalize the formant values, the primary difference is that it computes a single grand mean for all speakers included in the study (i.e. it's speaker-extrinsic, while Nearey is typically speaker-intrinsic). Also, unlike Nearey, it computes a scaling factor for each individual which is then used to modify each individual's vowel space rather than computing a set of non-Hertz-like values. In other words, since it is speaker-extrinsic, it is able to scale the original Hertz values as a part of its normalization process.

Implementation: NORM's implementation of the Labov method follows the formulas laid out by Labov, Ash, and Boberg (2006: 39-40). A logarithmic grand mean, G, is calculated from the geometric mean of the natural log of the F₁ and F₂ values of all vowels for all speakers. A logarithmic mean value, S, is then calculated for each speaker by taking the natural log of the F₁ and F₂ values for all of that speaker's vowels. The anti-log of the difference, G - S, is taken for F, the scaling factor for that speaker. Each individual's formant values are then multiplied by the scaling factor F to obtain her or his normalized values. (Apologies for not yet presenting the formula in mathematical notation; you may want to see the R script to better understand the implementation.)

Multiple Methods: NORM currently offers four versions of the Labov method. The first two output normalized mean values, while the second two output individual normalized values. The two sets are otherwise the same. The first in each, labeled speaker extrinsic, calculate the grand mean as described immediately above, using the speakers supplied in your uploaded spreadsheet. The using Telsur G value methods actually do not calculate the grand mean from your data. Instead they use the constant G = 6.896874 as the grand mean. This is the value Labov et al. (2006: 40) provide as their group mean for 345 American English speakers. In practice, the difference between the two Labov methods should simply affect the scaling - the specific Hertz values - of your output. Using the Labov ANAE method with the Telsur G value for American English data will presumably make your findings most comparable to the Atlas of North American English.

Advantages/Disadvantages: The Labov method has the same advantages and disadvantages as the Nearey formula. In addition, however, the practice of calculating a single grand mean for all speakers can introduce distortions of some normalized values. We observed quite noticeable distortions, especially for the vowel height scale, for certain comparisons of speakers in our sample datasets. As Labov, Ash, and Boberg (2006: 40) point out, G, the grand mean for all speakers, continues to change as the number of subjects increases. They found that above 345 subject the G value ceases to change significantly. This likely indicates that this method (and perhaps speaker-extrinsic methods in general) are best only when a study has an exceptionally high subject count.

---

Lobanov Method(s)

About: Lobanov's method was one of the earlier vowel-extrinsic formulas to appear, but it remains among the best.

Implementation: Following Nearey (1977) and Adank et al. (2004), NORM uses the formula (see the General Note below):

Fn[V]N = (Fn[V] - MEANn)/Sn

Where F_n[V]^N is the normalized value for F_n[V] (i.e., for formant n of vowel V). MEAN_n is the mean value for formant n for the speaker in question and S_n is the standard deviation for the speaker's formant n.

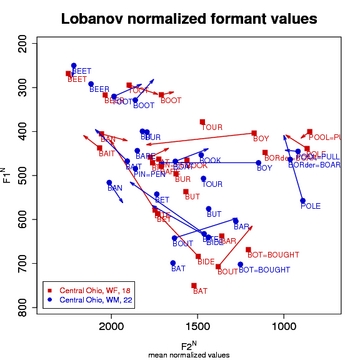Figure 3. Lobanov normalized vowels (scaled)

Multiple Methods: NORM currently offers four versions of the Lobanov method. The first, Lobanov, speaker intrinsic, uses the normal Lobanov method described above to generate mean normalized values. The second, Lobanov, indiv vowels, spkr intr, uses the normal Lobanov method described above to generate individual normalized values. The other two are available as experiments of sorts. The third, Lobanov, speaker extrinsic, computes a grand mean from all submitted speakers' vowels (n.b. it does the worst for small numbers of subjects). The fourth, Lobanov, means first, spkr intr, is speaker-intrinsic like the first, but computes the means of the un-normalized formant values and then normalizes those mean values instead of normalizing all of the vowels and then taking the means of those normalized values (n.b. you get different results than with the first).

Advantages/Disadvantages: The Lobanov method does an excellent job of factoring out physiologically-caused differences in formant values while retaining sociolinguistic differences. Moreover, Adank et al. (2004) found that, overall, it performed the best of all the techniques they tested in a discriminant analysis of normalized Dutch vowels (though only marginally better than Nearey's formula), was tied with Nearey in reducing physiological variation, and fared slightly worse than Nearey at preserving sociolinguistic variation. Disner (1980), however, who compared data from several languages, found that Lobanov was somewhat poorer than Nearey at reducing scatter in vowel measurements. She also noted that all of the vowel-extrinsic methods performed poorly at retaining "linguistic validity," that is, at preserving subtle language-specific differences in analogous vowels.

Lobanov makes attractive and easily readable plots that resemble F₁/F₂ formant plots. The results, however, are not in Hertz-like values so scaling is necessary to convert the normalized values to something more familiar (see the About Scaling section).

Lobanov has two main disadvantages. First, like other vowel-extrinsic formulas, it works optimally when all the vowels of speakers' vowel systems are included. When some vowels are excluded, vowel-extrinsic methods will yield skewed normalized values. This issue, of course, is a problem for researchers with tight time or budgetary constraints.

The other disadvantage, also shared with other vowel-extrinsic methods, is that it may be impaired when different dialects or languages that show different vowel systems are compared. For example, in the accompanying central Ohio dataset, the BOOT and BOAT vowels are strongly fronted, which causes the whole vowel system to be weighted toward front vowels. When this dialect is normalized together with another dialect that lacks this fronting, the normalized values for the central Ohioans are shifted slightly to the right (i.e., all the vowels are represented as slightly more backed than they should be).

General Note on Lobanov: Lobanov's (1971) publication, which introduced his method, actually reported using the rms (or root mean square) deviation and not the standard deviation for the denominator of the normalization formula. While the overall result of the formula is the same (since we're interested in the relative position of the vowels and the overall vowel space and not the actual numbers derived from the formula), it is unclear to the authors why Nearey (1977), Adank et al. (2004), and others report Lobanov's formula as using the standard deviation. Of course, for our implementation in NORM we've followed the preponderance of recent practice and also used the standard deviation.

---

Nearey Method(s)

Important Note: Until Oct. 13th 2008, NORM only implemented the Nearey2 formula (these methods were until then labeled simply as "Nearey"). NORM now also implements the Nearey1 formula, which has generally been found to be better (cf. Adank et al. 2004).

About: NORM implements two versions of the method that Terrance Nearey developed in his 1977 dissertation. The Nearey methods are vowel-extrinsic and in general rather similar to the Lobanov formula, though their formulae differ in that they normalize using log mean values. NORM follows Adank et al. (2004) in naming the major branches of the Nearey method Nearey1 and Nearey2.

Implementation: To normalize with the Nearey1 method, NORM uses the formula:

F*n[V] = anti-log(log(Fn[V]) - mean(log(Fn)))

Where F^*_n[V] is the normalized value for F_n[V], formant n of vowel V, and mean(log(F_n)) is the log-mean of all F_ns for the speaker in question.

To normalize with the Nearey2 method, NORM uses the formula:

F*n[V] = anti-log(log(Fn[V]) - MEANlog)

Where F^*_n[V] is the normalized value for F_n[V], formant n of vowel V, and MEAN_log is the log-mean of all F₁s and F₂s (and optionally F₃s; see next paragraph) for the speaker in question.

Put plainly, the difference between Nearey1 and Nearey2 is that Nearey1 is formant-intrinsic and Nearey2 is formant-extrinsic.

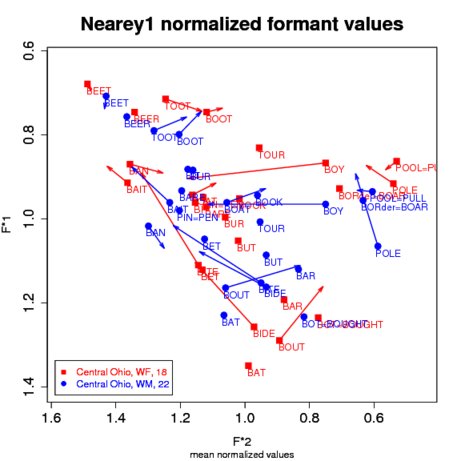Figure 4a. Nearey1 normalized vowels (unscaled)

Multiple Methods: NORM currently offers seven versions of the Nearey methods. The first, Nearey1 (formant intr), speaker intrinsic, uses Adank et al. (2004)'s preferred Nearey method and outputs mean values. The second, Nearey1, indiv vowels, spkr intr, uses this version of the method and outputs the individual normalized values. The third, Nearey1, indiv vowels, with F3s is like the previous (indiv) method, but also normalizes F3 values. The F3 values are not plotted in the output, but are included in output table. Since Nearey1 is formant-intrinsic, the Nearey1, indiv vowels, with F3s and the Nearey1, indiv vowels, spkr intr obtain the same normalized values for F1 and F2 - the plots will look the same. The fourth, fifth, and sixth Nearey methods - Nearey2 (formant extr), speaker intrinsic, Nearey2, indiv vowels, spkr intr, and Nearey2, indiv vowels, with F3s - are similar to the first three but calculate a grand mean based on all available formants.

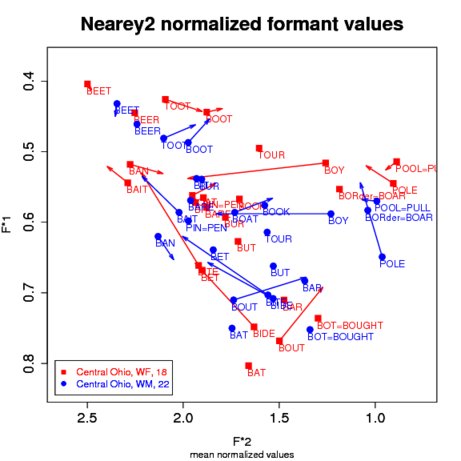Figure 4b. Nearey2 normalized vowels (unscaled)

The Nearey1, indiv vowels, with F3s and Nearey2, indiv vowels, with F3s methods are the only Nearey methods that normalize F3 values. Important: For Nearey2, indiv vowels, with F3s, the F3 values are included in the generation of the grand mean value - this gives different numeric results for F1 and F2 than when running Nearey2 without F3s; for this reason, you cannot compare speakers normalized with F3 values with those normalized without F3 values.

The final listed method, Nearey2, means first, spkr intr, is provided as an experimental alternative. It computes the means of the un-normalized formant values first and then runs the Nearey2 normalization algorithm on the mean values instead of normalizing all of the individual tokens and then taking the mean normalized values (n.b. this gives slightly different results than normalizing first and then taking the means). You probably don't want to use this method.

Advantages/Disadvantages: Much of what was said about the Lobanov formula also applies to Nearey. As noted above, Adank et al. (2004) found that it performed well in a discriminant analysis of normalized Dutch vowels in reducing physiological variation, and no worse than the other methods compared at preserving sociolinguistic variation. Disner (1980) found that it reduced scatter the best of all the methods she compared.

Like Lobanov, the Nearey formula yields attractive and easily readable plots of normalized values, but needs to be scaled to Hertz-like values (see About Scaling).

Nearey suffers from the same disadvantages as Lobanov. It performs best when the entire vowel system is included, which can be impractical for studies of many speakers. Use of fewer vowels will skew the normalized values. Furthermore, its effectiveness is slightly compromised when it is used to compare lects with different phonological inventories because, as noted above for Lobanov, some skewing of normalized values will result.

---

Watt & Fabricius Method

About: The Watt & Fabricius method is vowel-extrinsic, but unlike Lobanov's, Nearey's, and Labov's methods, the centroid or grand mean value that it uses to calculate normalized values is based on points that represent the corners of the vowel envelope: one for the high front corner, one for the high back corner, and one for the bottom corner. In Watt & Fabricius's original formulation, which was designed for the RP dialect of English, the mean F₁ and F₂ of the BEET vowel were used as the minimum F₁ and maximum F₂ values; the minimum F₁ value of BEET was also used as the minimum F₂ value. The mean F₁ and F₂ of BAT (which Watt and Fabricius label as TRAP) comprised the point for the bottom corner of the vowel envelope. Watt and Fabricius (2002) provide a clear step-by-step example of their process.

Implementation: We modified Watt & Fabricius's formulation in the following ways. First, we equated the minimum F₁ value with whichever mean F₁ happened to be lowest, whether or not it was the BEET vowel. Second, we did the same for the maximum F₂ value. Third, because the BAT vowel is not the one with the highest F₁ value in some American dialects (and in other languages), we assigned whichever vowel had the highest F₁ to be the point representing the bottom corner of the vowel envelope. Following Watt & Fabricius, we use the minimum F₁ value for both the F₁ and F₂ for, SCHOOL, the back-top corner of the vowel envelope. In other words, the S transforms, as Watt & Fabricius, call them are calculated thusly:

S(F1) = (BEETF1 + BATF1 + SCHOOLF1)/3 S(F2) = (BEETF2 + BATF2 + SCHOOLF2)/3

Where BEET and BAT stand for the acoustically measured top-front and bottom-middle of the vowel envelope and SCHOOL stands for the top-back corner, with SCHOOL_F1 and SCHOOL_F2 = BEET_F1 (as described above). Normalized values are then computed by dividing each vowel's mean F₁ and F₂ by the appropriate S transform. Finally, note that Watt & Fabricius operates on mean values - i.e., means of un-normalized formant values are computed first, and these means are normalized.

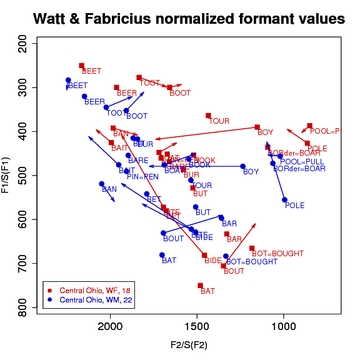Figure 5. Watt & Fabricius normalized vowels (scaled)

Advantages/Disadvantages: All the advantages and disadvantages described above for the Lobanov and Nearey techniques apply to Watt & Fabricius. In addition, however, this method also appears to show some distortion at the bottom of the vowel envelope. This problem appears to be due to the fact that some lects show a vowel at the very bottom point of the possible vowel space, while other lects instead show two parallel low vowels somewhat higher in the vowel space.